The PI-07P probe works in the frequency range 100 MHz – 60 GHz, covering most of the test requirements of MIL STD-464, RTCA-DO-160, FAA HIRF Rule & Advisory Circular 20-158, Boeing, Airbus and automotive EMC GM and Ford specifications.
in Pulse mode (with included PU-5P power unit) it measures the amplitude of pulsed RF fields from RF and microwave sources (microwave radars) with fast sampling detection capabilityof1 us (one microsecond). In Average mode it operates as standard isotropic field probe, measuring the RMS field strength of CW and AM/FM modulated signals.
Ultrabroadband isotropic electric field probe PI-07 extends the requirements of most EMC and RF safety standards for industrial, military and communication applications. It covers all RF and microwave frequency bands from MF up to M band, thus providing a versatile measuring tool for all 5G upcoming applications.
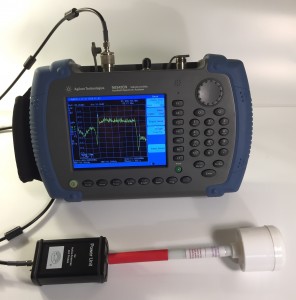
A unique broadband active E- field isotropic (spherically isotropic) antenna for RF spectrum monitoring. Connects to any spectrum analyzer, and has frequency response practically independent of antenna orientation or electric field direction. Offers high maximum field strength limit of 500 V/m and broad dynamic range for the variety of RF regulatory, safety, EMC, wireless and telecommunications applications. This antenna is a variant of OFA-G antenna but has about 20 dB higher overload limit and higher dynamic range.
Omnifield Antenna® consists of three parts: antenna head, handle and power unit. Antenna head and handle comprise a single module while power unit is detachable from the handle to allow convenient storage in the supplied rugged plastic case. For normal operation handle must be connected to the power unit to provide power to the antenna head. Antenna head has 3 antennas positioned normal to each other. Signals from each antenna are combined and amplified to allow utput signal of Omnifield Antenna® to be proportional to the absolute value of the field regardless of the field direction. Power unit contains the rechargeable battery and connectors for the antenna and output cable. Ferrite beads, located on this cable, decouple the antenna from spectrum analyzer and reduce the effects of this analyzer on measured field. This cable also allows operator to have freedom to place the antenna in right position either on non-metal table tripod (supplied with every system) or onto optional 5 feet adjustable tripod.
PI-SH (ICNIRP or FCC) is an isotropic electric field probe with shaped frequency response meeting the ICNIRP or FCC RF safety standards for occupational and general public exposure limits (see the specified frequency ranges below). Meter readings are shown in % of the STD – standard reference level, eliminating the need to know the source frequency. Probe output is proportional to RF power density in the whole specified power range, producing the correct RF power measurements in single and multi-signal environments, typically present at multiple antenna sites.
Isotropic Ultra Broadband Electric Field Probe PI-05 1 MHz- 40 GHz, 2 – 1000 V/m.
Modern design probe PI-05, extends the
requirements of most EMC and RF safety standards for industrial, military and
radar communication applications.
High overload field strength limit and
operation up to 40 GHz makes this probe a versatile measuring tool for all
applications including the microwave K-Band. This probe works with all RFP-05
type meters.
